Feature Importance

When working with complex features to train a machine learning model, the process to measure the feature importance is a crucial step. It allows us to better understand the feature data and, more importantly, it guides us in the feature selection process to simplify the machine learning model. Adding non-important features when training the model not only increases computational costs but also introduces a bias to the model.

The choice of the feature importance strategy is highly based on the data type and model that you are trying to implement. In this post, I will discuss some of the most common data-based strategies as well as more complex model-based strategies.

Data-Based Feature Importance

The choice of the data-based feature importance is highly dependent on the data type. Please refer to Jason Brownlee’s post below to find more information regarding different strategies for different input and output datatypes: https://machinelearningmastery.com/feature-selection-with-real-and-categorical-data/

In this post, I will be discussing two of the Data-Based Strategies: PCA and Spearman’s Coefficient.

I. PCA: Principal Component Analysis

Principal Component Analysis is a matrix dimension reduction method that allows evaluating feature importance by looking at the data’s first principal component. PCA method turns highly dimensional correlated data into uncorrelated smaller dimensional datasets. By using an orthogonal transformation, it creates the first component capturing most of the variance. I will show you how to implement PCA from scratch and how we could use it to find the feature importance. If the principal components of the PCA and the corresponding features have a high correlation, we can say that feature is relatively important and the feature well explains the overall variance in the dataset. This methodology is suitable for measuring numerical features’ importance (cannot be applied to a categorical variable).

In the section below, I will explain how to compute PCA step by step. As an example, I will be using the Iris Classification dataset from the Sklearn library. This dataset has four numerical features and the target variable has 3 classes. We will be transforming the 4-dimensional features into 2-dimensional space while maintaining most of the variances.

PCA Transformation From Scratch

# Importing Data
from sklearn import datasets

iris = datasets.load_iris()

X = iris.data
y = iris.target

One of the most important steps when implementing PCA is to scale the data. All the feature data needs to be scaled for the accurate interpretation of the feature importance. I used sklearn’s MinMaxScaler function below:

from sklearn import preprocessing as pp

scaler = pp.MinMaxScaler()
scaler.fit(X)
X_scaled = scaler.transform(X)

fig, axs =  plt.subplots(1, 2, figsize=(12,5))

colormap = np.array(['r', 'b', 'g'])

c=colormap[y]

axs[0].scatter(X_scaled[:,0], X_scaled[:,1], c=c)
axs[0].set_title('Distribution of Scaled \n 1st and 2nd Features', color = 'black', fontsize=16)

axs[0].spines['top'].set_visible(False)
axs[0].spines['right'].set_visible(False)


axs[1].scatter(X_scaled[:,2], X_scaled[:,3], c=c)
axs[1].set_title('Distribution of Scaled\n3rd and 4th Features', color = 'black', fontsize=16)

axs[1].spines['top'].set_visible(False)
axs[1].spines['right'].set_visible(False)

plt.show()

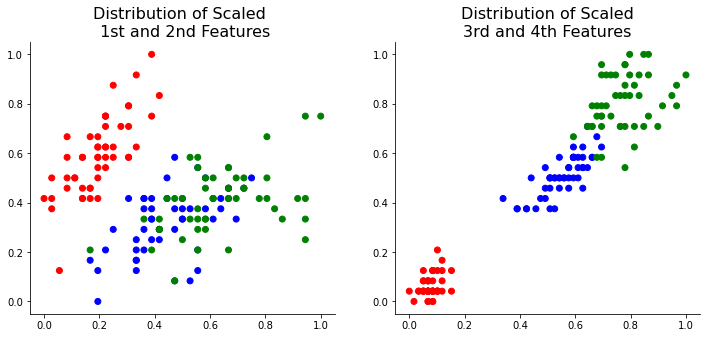
Now, let’s dive into PCA. The first step of PCA is to transfer the center point to 0 by subtracting the feature data’s mean. This step allows the center points of all the features to be the same.

X_trans = X_scaled - np.mean(X_scaled, axis = 0)

fig, axs =  plt.subplots(1, 2, figsize=(12,5))

axs[0].scatter(X_trans[:,0], X_trans[:,1], c=c)
axs[0].set_title('Re-Centered \n1st and 2nd Features', color = 'black', fontsize=16)
axs[0].spines['top'].set_visible(False)
axs[0].spines['right'].set_visible(False)


axs[1].scatter(X_trans[:,2], X_trans[:,3], c=c)
axs[1].set_title('Re-Centered \n3rd and 4th Features', color = 'black', fontsize=16)
axs[1].spines['top'].set_visible(False)
axs[1].spines['right'].set_visible(False)

plt.show()

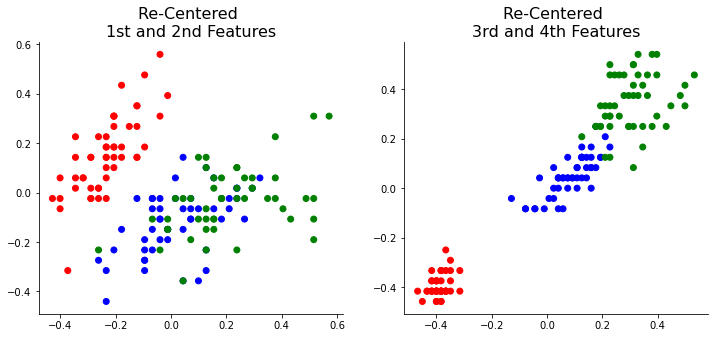
As you can see, the center points of the X_trans data are now at 0.

The second step is to calculate the covariance matrix from the transformed data. The covariance matrix is a square matrix giving the covariance between pairs of the element of given features.

And the third step is to calculate given values and eigenvectors of the covariance matrix

covariance = np.cov(X_trans , rowvar = False)
eig_values , eig_vectors = np.linalg.eigh(covariance)

Now, we can sort the eigen_values and eigenvalues by their eigenvalues.

After sorting, we need to take a dot product of the sorted transposed eigenvector and transformed feature data. This step transforms the high dimensional dataset into a lower dimensional space that the user specifies. For this example, I will reduce the dimension down to 2.

For more details, refere to article here: https://www.askpython.com/python/examples/principal-component-analysis

ind = np.argsort(eig_values)[::-1]
eig_values = eig_values[ind]
eig_vectors = eig_vectors[:,ind]
X_reduced = np.dot(eig_vectors[:,0:2].transpose() , X_trans.transpose() ).transpose()

# All the steps shown can be put together into a function as shown below
def PCA(X):
 
    X_trans = X_scaled - np.mean(X_scaled, axis = 0)
     
    covariance = np.cov(X_trans , rowvar = False)
    eig_values , eig_vectors = np.linalg.eigh(covariance)
     
    ind = np.argsort(eig_values)[::-1]

    eig_values = eig_values[ind]
    eig_vectors = eig_vectors[:,ind]

    X_red = np.dot(eig_vectors[:,0:2].transpose() , X_trans.transpose() ).transpose()
     
    return X_red, eig_vectors

X_reduced, eig_vectors = PCA(X_scaled)
eig_vectors

array([[-0.42494212,  0.42320271,  0.71357236,  0.36213001],
       [ 0.15074824,  0.90396711, -0.33631602, -0.21681781],
       [-0.61626702, -0.06038308,  0.0659003 , -0.78244872],
       [-0.64568888, -0.00983925, -0.61103451,  0.45784921]])

fig, ax =  plt.subplots(figsize=(6,5))

ax.scatter(X_reduced[:,0], X_reduced[:,1], c=c)
ax.set_title('PCA Dimensionaly Reduced Data (4D -> 2D)', color = 'black', fontsize=16)
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)

plt.show()

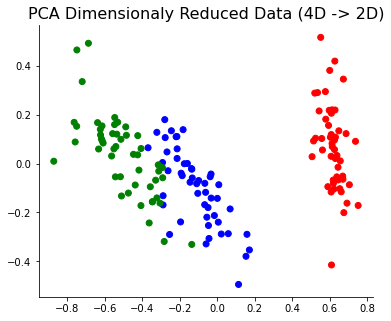
Since PCA reduced dataset now is able to obtain most of its information with the 2D space, we could see the 3 label groups more clearly.

PCA Feature Importance Calculation Using Sklearn

Now, we can use the eigenvector calculated from above to show how much of the variance in the original data is explained by each of the features. For the next steps, I will be using sklearn’s PCA library. With sklearn’s PCA library, you can easily compute PCA components and use expained_variance_ratio to calculate feature importance.

from sklearn.decomposition import PCA

pca = PCA().fit(X_scaled)
print(pca.components_)

[[ 0.42494212 -0.15074824  0.61626702  0.64568888]
 [ 0.42320271  0.90396711 -0.06038308 -0.00983925]
 [-0.71357236  0.33631602 -0.0659003   0.61103451]
 [-0.36213001  0.21681781  0.78244872 -0.45784921]]

As you can see, the pca. components_ is the same as the eigenvector that we manually calculated from the steps above.

Now let’s plot the cumulative explained_varaince_ratio that explains the percent of the variance that each of your data explains.

fig, ax =  plt.subplots(figsize=(8,5))

ax.bar(['First','Second','Third','Fourth'],pca.explained_variance_ratio_*100, color ='#A40227')
ax.set_title('Percent of the Variance Explained\nby Each Principal Component', color = 'black', fontsize=14)
ax.set_xlabel('Pricipal Components', color = 'black', size = 13)
ax.set_ylabel('Percent of Variance Explained', color = 'black', size = 13)

ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)

plt.show()

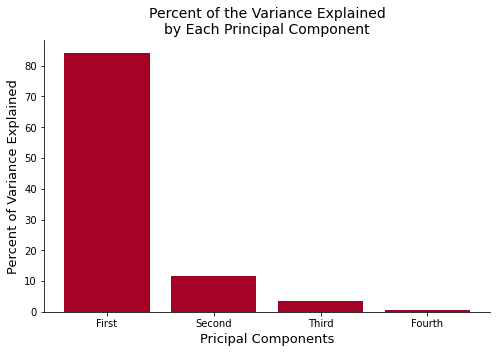
The plot above shows that the first principal component explains more than 70 percent of the variance in the data. Since the first component explains the majority of the variance, we can take a look into the component and determine which feature is important. Let’s use this variance-ratio and calculated eigenvector to compute the feature importance.

output = pd.DataFrame(
    data=pca.components_.T * np.sqrt(pca.explained_variance_), 
    columns=[f'PC{i}' for i in range(1, X_scaled.shape[1] + 1)],
    index = ['Feature 1', 'Feature 2', 'Feature 3', 'Feature 4']
)

pc1_output = output.sort_values(by='PC1', ascending=False)[['PC1']]
pc1_output = pc1_output.reset_index()
pc1_output.columns = ['Att', 'PC1_C']

plot_feat_imp( pc1_output['Att'], pc1_output['PC1_C'], "PCA's First Component Feature Importance")

# https://towardsdatascience.com/3-essential-ways-to-calculate-feature-importance-in-python-2f9149592155

The plot above shows the loading score which measures how much the feature can capture the first component’s variance. The plot shows that Feature 3, 4, and 1 are important, but Feature 2 is not so significant.

II. Spearman’s Rank Correlation Coefficient

Another simple feature importance strategy is to analyze the feature’s Spearman’s Rank Correlation Coefficient against its target variable. The Spearman’s Rank Correlation Coefficient measures the degree to which ranked values of the two variable is associated by a monotonic function. Since it uses ranking and access monotonic relationship, it can capture a wider range of correlation compared to traditional Pearson’s correlation (which assess linear relationship).

Since Spearman’s Rank Correlation uses numerical values of the feature and the target variable, we can only use this strategy between numerical variables. Therefore, we cannot use the Iris dataset that is used before. In the example below, I used Scipy’s Spearmanr function to find the feature importance of the UCI Machine Learning Lab’s Wine dataset. I have chosen a subset of the features for simplicity

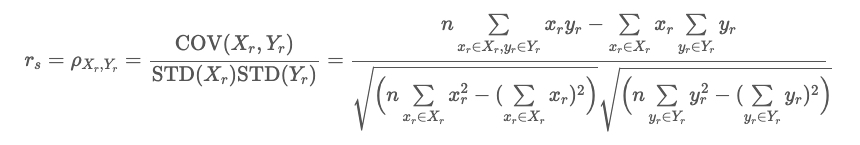
# Importing Wine Data
df_wine = pd.read_csv('./data/winequality-white.csv', sep = ';')
df_wine['random'] = np.random.random(size=len(df_wine))

# # Normalize The Numerical Columns
y = df_wine['quality'].copy()
df_wine = (df_wine-df_wine.min())/(df_wine.max()-df_wine.min())
df_wine['quality'] = y


df_wine.head()

	fixed acidity	volatile acidity	citric acid	residual sugar	chlorides	free sulfur dioxide	total sulfur dioxide	density	pH	sulphates	alcohol	quality	random
0	0.307692	0.186275	0.216867	0.308282	0.106825	0.149826	0.373550	0.267785	0.254545	0.267442	0.129032	6	0.692127
1	0.240385	0.215686	0.204819	0.015337	0.118694	0.041812	0.285383	0.132832	0.527273	0.313953	0.241935	6	0.190148
2	0.413462	0.196078	0.240964	0.096626	0.121662	0.097561	0.204176	0.154039	0.490909	0.255814	0.338710	6	0.008613
3	0.326923	0.147059	0.192771	0.121166	0.145401	0.156794	0.410673	0.163678	0.427273	0.209302	0.306452	6	0.470798
4	0.326923	0.147059	0.192771	0.121166	0.145401	0.156794	0.410673	0.163678	0.427273	0.209302	0.306452	6	0.960827

df_wine_subset = df_wine[['quality','citric acid', 'residual sugar', 'fixed acidity', 'chlorides', 'free sulfur dioxide', 'alcohol', 'pH', 'random']]

X = df_wine_subset.drop('quality', axis = 1)
y = df_wine_subset['quality']
labels = list(X.columns)

results = calculate_spearman(labels, X, y)

Spearman's Coefficient of citric acid: 0.018 (p-value = 0.19955893)
Spearman's Coefficient of residual sugar: -0.082 (p-value = 1e-08)
Spearman's Coefficient of fixed acidity: -0.084 (p-value = 0.0)
Spearman's Coefficient of chlorides: -0.314 (p-value = 0.0)
Spearman's Coefficient of free sulfur dioxide: 0.024 (p-value = 0.09703376)
Spearman's Coefficient of alcohol: 0.44 (p-value = 0.0)
Spearman's Coefficient of pH: 0.109 (p-value = 0.0)
Spearman's Coefficient of random: 0.008 (p-value = 0.59359146)

plot_feat_imp(list(results.keys()), list(results.values()), "Spearman's Feature Importance")

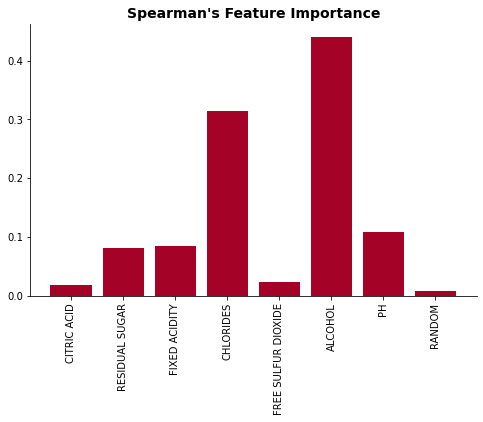
As the importance plot shows, alcohol and chlorides concentration had the highest Spearman’s coefficient. This implies that alcohol and cholorides concentration is most highly correlated to the target variable (quality of wine). And Random, Citric Acid, and Free Sulfur Dioxide are shown to be uncorrelated to the target variable.

Model Based Feature Importance

A more direct and accurate way of capturing the feature importance is to use the model-based feature importance methodologies. While data-based feature importance provides a quick and easy check on the feature importance, it fails to capture the importance of features with more complex relationships. Also, which works wells for the numerical variables, it is more difficult for data-based strategies to be applied to categorical features.

The model-based feature importance users the ML models to directly measure the increase and decrease in one of its metrics or performances. We will be taking a look into the following strategies:

• Impurity (Gini) Method
• Permutation Method
• Drop One Column Method
• SHAP
• RFPIMP Method

I. Random Forest’s Mean Impurity Decrease Score

The default feature importance method for the scikit-learn library is the impurity score method. It measures the mean drop of the Gini score to indirectly measure the feature importance. Since the RF algorithm uses a Gini score (impurity) to select the feature and develop each node, the impurity score is a quick and easy method to evaluate each feature’s importance.

Cutler and Breiman who are the inventors of the Random Forest Algorithm state that the Gini drop method “gives a fast variable importance that is often consistent with the permutation importance measure.” Even though this is an extremely fast method to implement, it doesn’t always provide accurate feature importance. Due to the nature of the Gini score calculation, the method usually provides a higher score for the numerical features compared to that of categorical features. This bias could provide a wrong conclusion regarding the feature’s importance.

Now, let’s take a look into how it is implemented using sklearn’s library

from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_squared_error

def impurity_imp(X, y, n_iter=5):
    
    imp_dict = dict.fromkeys(X.columns,0)
    
    for i in range(n_iter):
        rf = RandomForestRegressor(
             n_estimators=500,
             min_samples_leaf=5,
             n_jobs=-1,
             max_depth = 60,
             oob_score=True,
             random_state= i + 5)
        
        rf.fit(X,y)
        
        for i, col in enumerate(X.columns):
            imp_dict[col] += rf.feature_importances_[i]
    
    for key in imp_dict:
        imp_dict[key] = imp_dict[key]/n_iter
    
    return imp_dict
        

impurity_dict = impurity_imp(X, y, n_iter=30) # Iterated 30 times and averaged for accuracy

plot_feat_imp(list(impurity_dict.keys()), list(impurity_dict.values()), "RF's Mean Impurity Decrease  Importance")

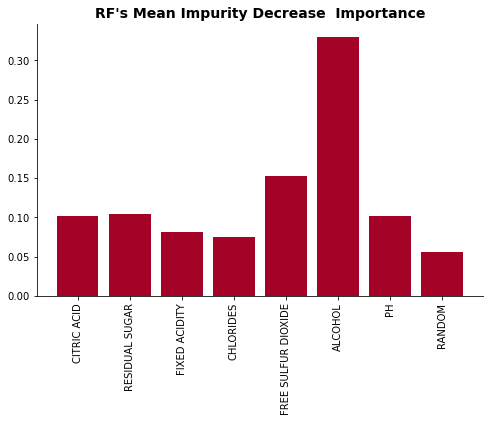
II. Permutation Importance

Another common and fast model-based feature importance method is permutation importance. The idea behind the permutation importance is fairly simple.

1. Train a model (in this case Random Forest was used) using a training dataset.
2. Predict using the trained model on the validation dataset and calculate the error (MSE). This error is the baseline error.
3. Randomly shuffle (permutation) one of the feature columns.
4. Create another prediction (y_hat) using the model trained in step 1 and calculate a new error.
5. Calculate the increase in the error (new_error - baseline_error)
6. Repeat steps 3 - 6 by shuffling one column at a time.

Since the method measures how much the error has increased after randomizing one of the features, it shows how much the developed model relies on the feature for its prediction. If the feature didn’t seem to be important when training an RF model, shuffling the feature would not impact the performance of the model. However, if the RF model relies heavily on the feature for its prediction, the random shuffle of the feature will impact the model performance significantly.

This is another fairly quick method since you only need to train the model once. However, if the dataset has highly-correlated features, the method could say that one of the features is not important.

For the full algorithm, please refer to the featimp.py file attached.

rf = RandomForestRegressor(
         n_estimators=500,
         min_samples_leaf=5,
         n_jobs=-1,
         max_depth = 60,
         oob_score=True)

perm_dict = permutation_imp(rf, X, y, n_iter=30)

plot_feat_imp(list(perm_dict.keys()), list(perm_dict.values()), 'Permutation Feature Importance')

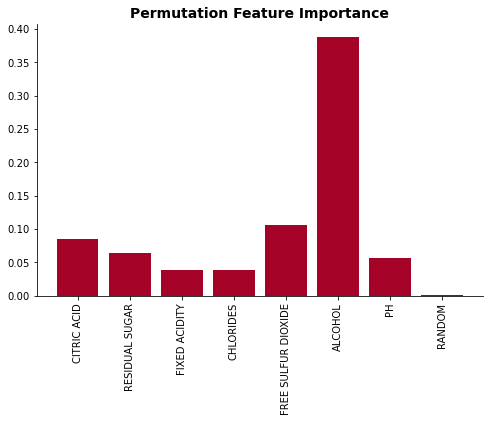
Now let’s take a look into what would happen when we add highly-correlated feature to the data. I will create ‘free sulfur dioxide2’ feature which is same as the ‘free sulfur dioxide’ feature.

X_dup = X.copy()

X_dup['free sulfur dioxide2'] = X_dup['free sulfur dioxide']

perm_dict = permutation_imp(rf, X_dup, y, n_iter=30)
plot_feat_imp(list(perm_dict.keys()), list(perm_dict.values()), 'Permutation Feature Importance With A Duplicated Feature')

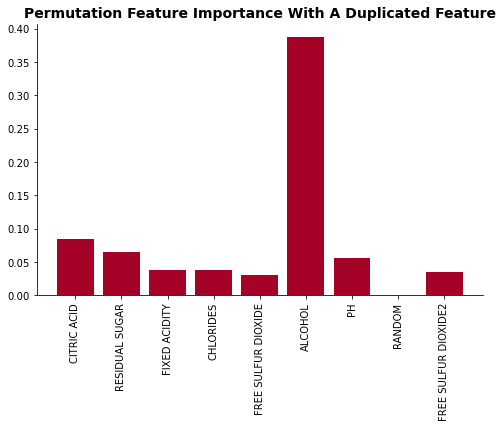
As the feature importance plot shows, adding a duplicated feature significantly decrease it’s feature importance. The Free Sulfur Dioxide feature’s importance dropped from 2nd highest to 5th.

III. Drop-Column Importance

The more computation-heavy but generally more accurate version of the permutation method is the drop-column importance. While the permutation and impurity drop method only requires training of the model once, the drop-column method requires new training of the model for every feature evaluated. Therefore, in order to train a complex model on a large amount of data, this method is extremely computation heavy. These are the general steps of the drop-column method:

1. Train a model (in this case Random Forest was used) using a training dataset.
2. Predict using the trained model on the validation dataset and calculate the error (MSE). This error is the baseline error.
3. Drop one feature and train the model and evaluate (new error).
4. Calculate the increase in the error (new_error - baseline_error) with the drop of the feature.
5. Repeat steps 3 - 6 for every feature to be evaluated.

The algorithm is very straightforward and it can be implemented with most of the ML models. However, since we are dropping one feature at a time, this method also suffers when highly correlated features are present.

rf = RandomForestRegressor(
         n_estimators=200,
         min_samples_leaf=5,
         n_jobs=-1,
         max_depth = 60,
         oob_score=True)

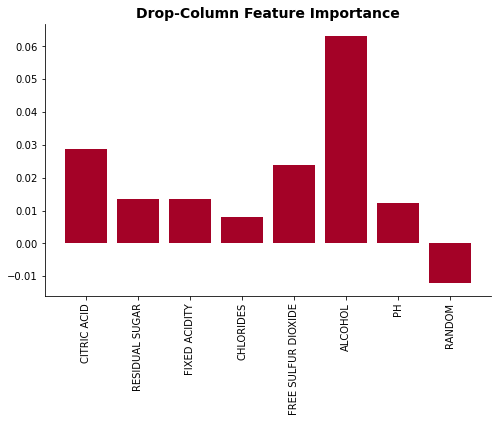
drop_dict = drop_one_imp(rf, X, y)

plot_feat_imp(list(drop_dict.keys()), list(drop_dict.values()), 'Drop-Column Feature Importance')

drop_dict = drop_one_imp(rf, X_dup, y)
plot_feat_imp(list(drop_dict.keys()), list(drop_dict.values()), 'Drop-Column Feature Importance With A Duplicated Feature')

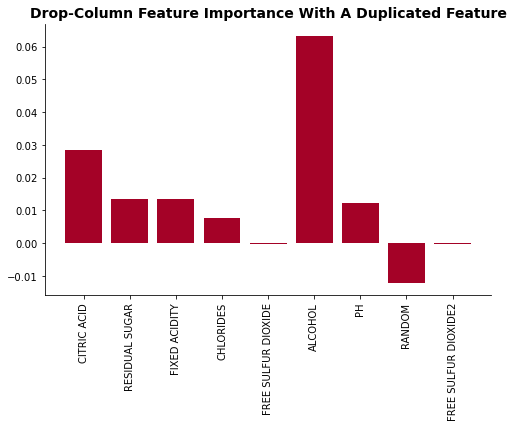
As the feature importance plot shows, adding a duplicated feature significantly decrease it’s feature importance. The Free Sulfur Dioxide feature’s importance dropped from 2nd highest to 5th.

IV. SHAP

Another alternative method of permutation feature importance method is SHAP feature importance. It is similar to the permutation method in that it uses the permutation of a feature. However, to calculate the importance based on the magnitude of feature attributions instead of the decrease in the model performance. The method uses “shapley value” based on coalition game theory which was first developed by Lundberg and Lee in 2017. They suggested this new method which has both “consistency” and “accuracy”. “The feature values of a data instance act as players in a coalition. Shapley values tell us how to fairly distribute the “payout” (= the prediction) among the features”

Please refer to https://christophm.github.io/interpretable-ml-book/shap.html for more detailed explaintion of the algorithm.

import shap

rf = RandomForestRegressor(
         n_estimators=500,
         min_samples_leaf=5,
         n_jobs=-1,
         max_depth = 60,
         oob_score=True)

rf.fit(X,y)


shap_values = shap.TreeExplainer(rf).shap_values(X)

plot_feat_imp(list(X.columns), np.mean(np.abs(shap_values), axis=0), 'SHAP Feature Importance')

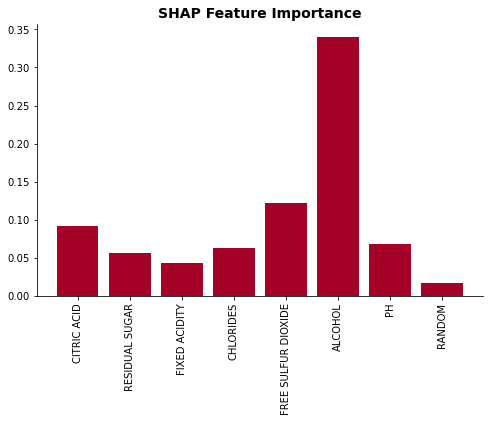
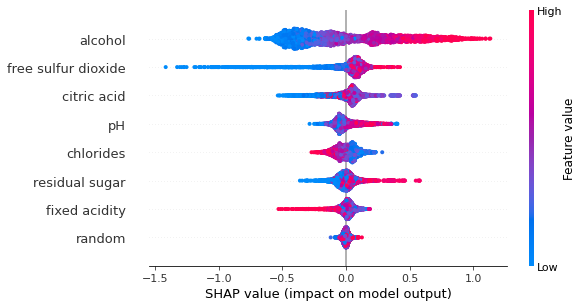
f = plt.figure()
shap.summary_plot(shap_values, X)

rf = RandomForestRegressor(
         n_estimators=500,
         min_samples_leaf=5,
         n_jobs=-1,
         max_depth = 60,
         oob_score=True)

rf.fit(X_dup,y)


shap_values = shap.TreeExplainer(rf).shap_values(X_dup)
plot_feat_imp(list(X_dup.columns), np.mean(np.abs(shap_values), axis=0), 'SHAP Feature Importance')

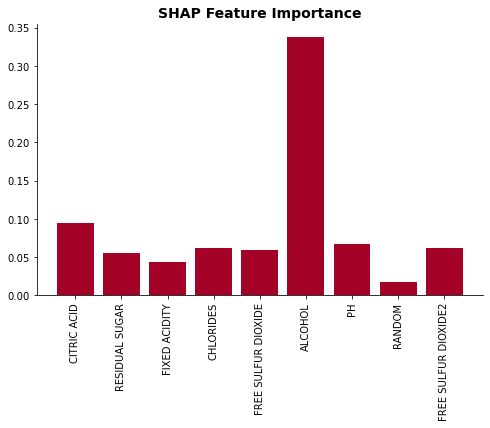
While duplicated features does suffers even with SHAP method, the decrease in the importance is significanly less than that of permuation and drop-column methods.

V. RFPIMP

This is a feature importance package developed by Terence Parr and Kerem Turgutlu. This package features different types of common feature importance methods like permatation and drop column.

Refer to the source code here for futher information: https://github.com/parrt/random-forest-importances/blob/master/src/rfpimp.py#L23

from rfpimp import *

rf = RandomForestRegressor(
         n_estimators=500,
         min_samples_leaf=5,
         n_jobs=-1,
         max_depth = 60,
         oob_score=True)

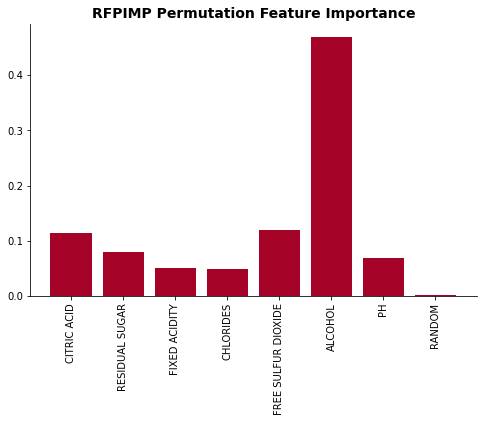
rfpimp_dict = rfpimp_imp(rf, X, y, n_iter=5, split_prop = 0.8)

plot_feat_imp(X.columns, list(rfpimp_dict.values()), 'RFPIMP Permutation Feature Importance')

viz = plot_corr_heatmap(X, figsize=(7,5))
viz.view()

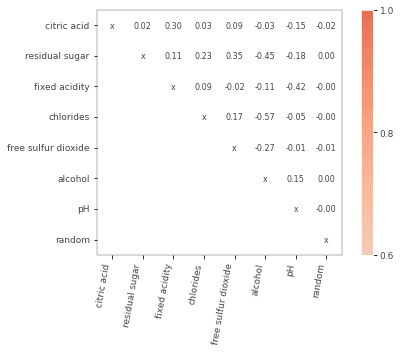
The package has very useful correlation heatmap that allows users to easily identify collinear features.

Comparing Strategies

There are pros and cons for all the methods that I discussed above. Now let’s compare their performance and see how their feature selection is accurate. In order to evaluate each method’s performance, I have calculated the error of the top n important features selected for each method.

The plot below shows how each method’s selection performs with its top n features. As you can see, SHAP, impurity, and permutation method performs the best initially. As the number of top n important feature is increased, all of the method’s model converges to a lower error.

X = df_wine.drop('quality', axis = 1)
y = df_wine['quality']

combined_dict = feat_imp_list_creator(X, y, 10)

error_combined = error_calc(X, y, combined_dict)

fig, ax =  plt.subplots(figsize=(8,5))

for method in error_combined:
ax.plot(range(len(error_combined[method])), error_combined[method], label = method)
ax.set_title('Feature Importance Method Comparison', color = 'black', fontsize=14)

ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)

ax.legend()

plt.show()

Null Importance - Finding Important Features

There is some chance that the evaluated feature importance by different methods could be due to a chance. In order to prevent bias in the selection of feature importance, we could bootstrap the method and calculate a 95% confidence interval.

In order to ensure that the feature provides some prediction relevance to the model, we could create arbitrary feature importance using a random dataset. And compare it to the value of the importance and see if the calculated feature importance could be purely due to a chance. In the plots below, I have calculated random feature importance 60 times to compare it to a few of the features.

rf = RandomForestRegressor(
         n_estimators=200,
         min_samples_leaf=5,
         n_jobs=-1,
         max_depth = 60,
         oob_score=True)
act_imp = permutation_imp(rf, X, y, n_iter = 20)

null_imp_comb = {}

for col in list(X.columns):
    null_imp_comb[col] = []
    
nb_runs = 60
y_ = y.copy()

for i in range(nb_runs):

    y_ = y_.copy().sample(frac = 1, random_state = i + 100)
    null_imp = permutation_imp(rf, X, y_, n_iter = 1)
    for key in null_imp:
        null_imp_comb[key].append(null_imp[key])

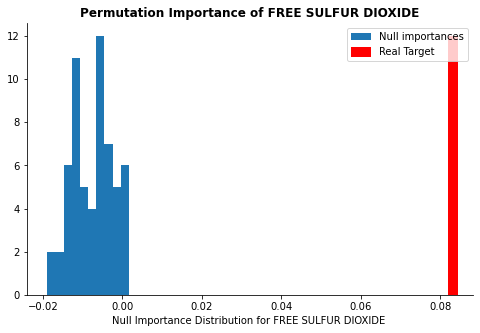
display_distributions(act_imp, null_imp_comb, 'free sulfur dioxide')

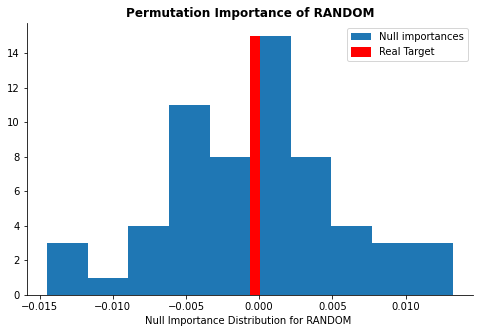
display_distributions(act_imp, null_imp_comb, 'random')

display_distributions(act_imp, null_imp_comb, 'alcohol')

The plots above show whether the calculated feature importance might be purely due to a chance. The red line represents the calculated feature importance value and the blue distribution represents feature importance calculated from the null dataset. If the red line is far away from the rest of the blue distribution, it implies that the feature importance is significant and should be kept in the model. As you can see, while free sulfer dioxide and alcohol concentrations are far away from the null distribution, the random feature is well within the distribution.

Variance and Emperical p-values

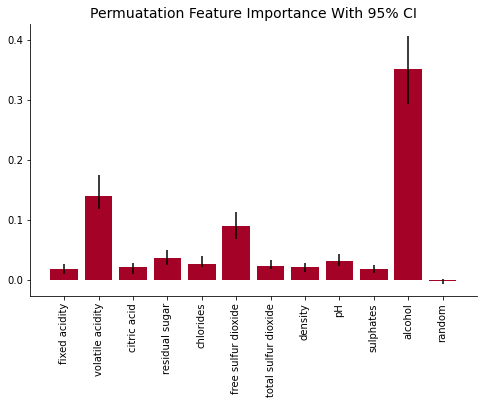
Another method to evaluate the calculated feature importance is to implement a bootstrap method. By using a bootstrap method we could calculate each score’s 95% confidence interval. If the 95% CI includes a value of 0, we cannot conclude that the feature shows any improvement to the model with 95% confidence. If the feature’s interval is above 0, we can conclude that the feature shows some significance when predicting its target with 95% confidence.

rf = RandomForestRegressor(
         n_estimators=200,
         min_samples_leaf=5,
         n_jobs=-1,
         max_depth = 60,
         oob_score=True)

imp_comb = {}
for col in list(X.columns):
    imp_comb[col] = []
nb_runs = 80
y_ = y.copy()

for i in range(nb_runs):
    imp = permutation_imp(rf, X, y_, n_iter = 1, seed = i*2)
    for key in imp:
        imp_comb[key].append(imp[key])

low_perc = 2.5
high_perc = 97.5

low_error = []
high_error = []
modes = []
key_list = []
for key in imp_comb:
    
    low_value = np.percentile(imp_comb[key],low_perc)
    high_value = np.percentile(imp_comb[key],high_perc)
    mode = np.percentile(imp_comb[key],50)
    
    key_list.append(key)
    modes.append(mode)
    low_error.append(mode - low_value)
    high_error.append(high_value - mode)

plot_feat_imp(key_list, modes, 'Permuatation Feature Importance With 95% CI', yerr = (low_error, high_error))

Conclusion

Throughout this post, I have shown how different methods could be implemented in order to find each feature’s important when building a model. As shown, each method has some pros and cons and it should be carefully selected considering your need and data type. In addition, by considering the bootstrap method, you can evaluate the calculated feature importance to build the confidence interval of the feature importance. By using these strategies, you can build the model with features that not only decrease the computational time but increase its performance by decreasing the bias in the data.