K-Means Clustering

What is Clustering?

Clustering is an unsupervised machine learning technique to group similar data by only using input features. The dataset in the same cluster should share some similar behavior or high intra-cluster similarity. We can use the group directly to predict or feed it to a model as a feature set.

Most of the clustering process is unsupervised learning, which means that the algorithm learns from the data without any labels. This is similar to how humans perceive and process the world. For example, when we study animals, we first divide living organisms into different taxonomical kingdoms according to their biological characteristics. Species in the same kingdom share similar biological properties that are not found in another kingdom. Similar to taxonomy, the process of clustering allows the algorithm to divide data into different clusters by analyzing its features.

What is K-Means?

K-Means is one of the most common types of clustering technique where the algorithm divides the data into K number of groups. It is popular due to its simplicity and interpretability. It divides the data by minimizing the sum of the distance between each data mean/centroid of its cluster.

The diagram below shows data with 3 clusters. Three large dots (red, blue, and green) represents the centroids of the cluster. And three-color region represents which centroids the location is closest to and the data with the same closest centroid belongs to the same group.

image source: https://www.naftaliharris.com/blog/visualizing-k-means-clustering/

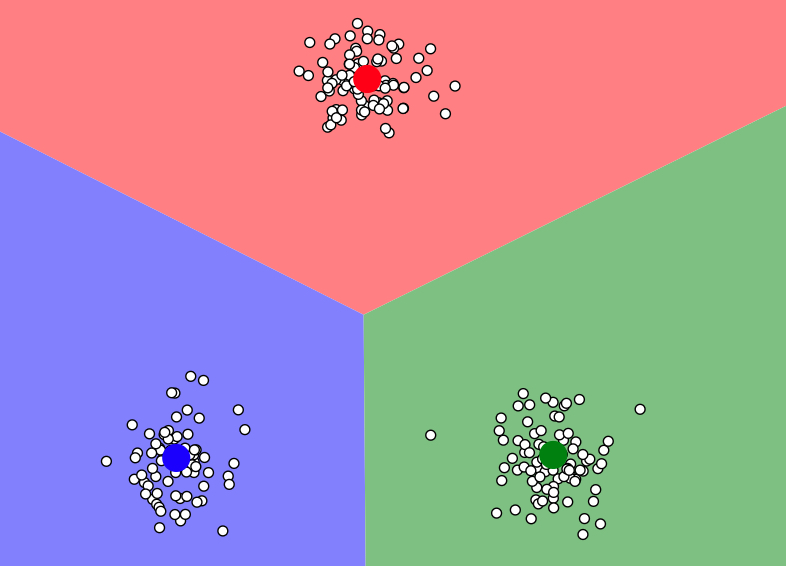
How does K-Means algorithm group data into k-clusters?

To assign each data into a group, the K-Means algorithm calculates “similarities” between the data. The “similarity” is calculated by examining distances between the points. There are several methods to calculate the distance, but the most common method is Euclidean Distance. The following is the equation for Euclidean Distance in 2-dimensional space:

\[Euclidean Distance = \sqrt{(X_2 - X_1)^2 + (Y_2 - Y_1)^2}\]

You might have already noticed, but this equation is identical to the Pythagorean theorem and it is sometimes referred to as Pythagorean distance. In other words, the Euclidean distance calculates the minimal geometrical distance between the two points. The goal of the K-Means is to minimize this distance between data and k different centroids.

K-Mean Algorithm

In general, the K-Means algorithm follows these steps to identify each cluster:

1. Initiation: Initiate K-Mean by randomly selecting k unique points from data as initial centroids of k clusters.
2. Cluster Assignment: Calculate the distance between given data and centroids and assign each record (x) to the cluster with minimum distance.
3. Cluster Update: Update centroids of clusters by mean of records in each cluster.
4. Iteration: Repeat steps 2 and 3 until the clusters don’t change.

In the next section, I will explain each step more in detail with examples.

Step 1: Initiation

To initiate the K-Mean clustering, we randomly selecting k data from input matrix X as centroids. This k centroids will serve as our initial guess of the clusters. This process can be optimized by the “K-Means++” method which I will discuss later in this report.

In the example below, I have generated random 20 records of data with 4 features as a simple example. Since k=3, we have pulled 3 different records as initial centroids.

k = 3 # Number of clusters
X = np.random.randint(100,size = (20,4))

# Randomly choosing inital centroids
c_ind = np.random.choice(X.shape[0],k,replace = False)
C = X[c_ind]
print('3 initial centroids: \n', C)

3 initial centroids: [[74 12 78 53] [51 40 23 57] [89 17 3 10]]

Step 2: Cluster Assignment

We can now assign each record to a cluster with minimum distance. The minimum distance is calculated using numpy.linalg.norm() function, which is equivalent to the Euclidean Distance. For each record, calculate the distance between k centroids that was chosen in the previous step. The record is assigned to a cluster with a minimum distance to its centroid.

clusters = np.zeros(X.shape[0]).astype(int)

for i, row in enumerate(X):
    
    min_dist = float('inf') 
    
    for cid, c in enumerate(C):
        euc_dist = np.linalg.norm(row - c) # Euclidean Distance Calculation to c centroid
        
        if euc_dist < min_dist: # If the distance is smaller than the distance previous calculated, assign the record to c cluster.
            min_dist = euc_dist
            clusters[i] = cid

print('Cluster assigned to each records: ', clusters)

Cluster assigned to each records: [1 1 0 1 1 1 0 0 0 2 1 0 1 1 0 1 0 0 0 0]

Step 3: Cluster Update

After assigning all records to clusters, we will now update each cluster’s centroid by taking the average of assigned records. This will incrementally relocate centroids of clusters to more appropriate positions. As you can see below, the centroids of three clusters C have been updated.

for i in range(k): 
    C[i] = X[clusters == i].mean(axis=0)
    
print(C)

[[50 32 81 45]
 [38 53 55 68]
 [89 17  3 10]]

Step 4: Iteration

Repeat steps 2 and 3 until either max number of iterations has reached or if it has failed to relocate the cluster. The fact that the cluster has stopped updating the cluster indicates that the K-Means algorithm has found a local minimum of Euclidean distance. Since the algorithm doesn’t guarantee finding the most optimal solution (global minimums), it is suggested to run this process several times. One complete cycle of K-Means clustering is defined below:

def kmeans_base(X, k, max_iter = 30, tolerance = 1e-2):
    
    clusters = np.zeros(X.shape[0]).astype(int)

    c_ind = np.random.choice(X.shape[0],k,replace = False)
    C = X[c_ind]
    
    C_prev = np.zeros(C.shape)

    for m in range(max_iter):
        for i, row in enumerate(X):
            min_dist = float('inf')
            min_clust = -1
            for cid, c in enumerate(C):
                euc_dist = np.linalg.norm(row - c)
                if euc_dist < min_dist:
                    min_dist = euc_dist
                    clusters[i] = cid
        for i in range(k):
            C[i] = X[clusters == i].mean(axis=0)

        if (abs(C_prev-C)< 1e-2).all():
            print(f'Ended at iteration {m}')
            return C, clusters
        
        C_prev = C.copy()
    
    print(f'Max Iteration Reached')
    return C, clusters

Iris Example

Let’s run the K-Means function with the Iris classification problem. The dataset contains four numerical features corresponding to measurements of pedal and sepals of the Iris flowers. And it contains 3 species of Iris as labels (0, 1, 2). Now, let’s use our K-Means Algorithms to predict species of Iris with its features.

Since we already know that there are only three labels exist in the dataset, we will assign k = 3. In the later section below, we will discuss a method to choose the best k value.

image source: https://machinelearninghd.com/iris-dataset-uci-machine-learning-repository-project/ “

from sklearn import datasets
# Loading Data
Iris = datasets.load_iris()
X = Iris.data
y = Iris.target

# Running K-Means With k = 3
np.random.seed(1)

centroids, labels = kmeans(X, 3)

Ended at iteration 11

accuracy = sum(labels == y) / len(y)
print('K-Means Prediction Accuracy: ', round(accuracy,2))

K-Means Prediction Accuracy:  0.89

As you can see, our simple K-Mean clustering was able to predict the label with high accuracy of 89 percent.

K-Means Initiation Problem

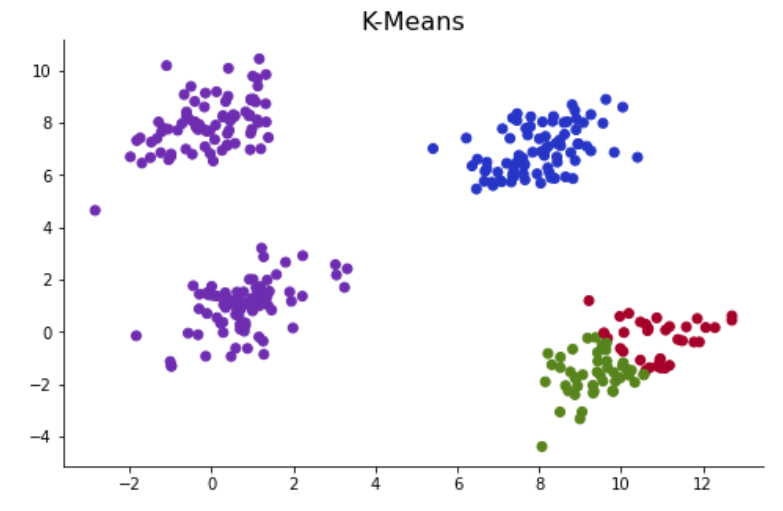
Outputs of the K-Mean clustering algorithm are highly impacted by the initial centroids that it chooses. The initial placement of the centroids highly impacts convergence rate and accuracy. As an example, I have generated a synthetic dataset with four clusters. Since four clusters are clearly grouped, the K-Mean algorithm identifies these four groups correctly in most cases. However, when K-Means initiates with initial centroids set to close to each other, it incorrectly classifies the clusters.

# Generating Syntheic Data
means = [[1,1], [8, 7], [0,8], [10,-1]]
data = random_cluster_data(n_clusters = 4, means = means)

colors=np.array(['#2135CA','#A40227', '#598413', '#6C2DB3'])

fig, ax = plt.subplots(figsize=(8,5))  

ax.scatter(data[:,0],data[:,1])
ax.set_title('Synthetic Data', color = 'black', fontsize=16)

ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)

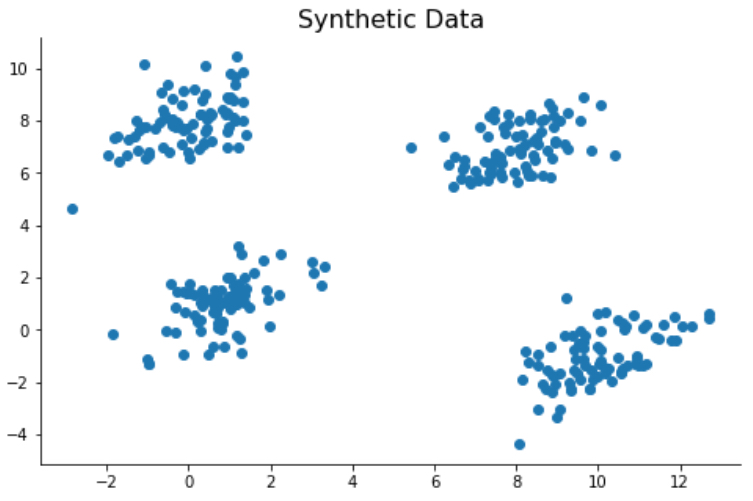
# Running K-Means with k =4  until misclassification
np.random.seed(2)

centroids, labels = kmeans(X = data, k = 4)

Ended at iteration 3

colors=np.array(['#A40227', '#598413', '#6C2DB3','#2135CA'])

fig, ax = plt.subplots(figsize=(8,5))  

ax.scatter(data[:,0],data[:,1], color = colors[labels])
ax.set_title('K-Means', color = 'black', fontsize=16)
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)

K-Means++

K-Means++ algorithm tackles this initiation problem by optimizing the initiation of centroids. The only difference between K-Mean and K-Mean++ algorithms differs in the centroid initiation method. While K-Mean initialized centroids with complete random selection, K-Means++ chooses centroids that maximize the minimum distance between centroids and records.

1. Like the basic K-Means algorithm, choose the first centroids randomly
2. For each point compute distances between the point and the centroid(s). Record the minimum distance among those.
3. Repeat step 2 for all points, and choose a point that maximizes the minimum distance
4. Repeat steps 2 and 3 until k centroids are chosen

def select_centroids_(X,k):
    """
    Chooses k centroids by using K-Means+++ method
    """
    first_c_ind = np.random.choice(X.shape[0],1) # Randomly Choose The First Centroid
    
    C = X[first_c_ind]
    
    for k_ in range(k-1):
        
        index_max_dist = -1
        max_dist = 0

        for i, row in enumerate(X): 
            
            min_dist = float('inf')

            for cid, c in enumerate(C):

                euc_dist = np.linalg.norm(row - c) # Calculate Euclidean between data point and all previous centroids

                if euc_dist < min_dist:
                    new_c = c
                    min_dist = euc_dist

            if min_dist > max_dist: # Find point with maximum distance, which will become one of the initial centroids
                max_dist = min_dist
                index_max_dist = i

        C = np.vstack([C,X[index_max_dist]]) # Add new centroids to C
        
    return C

# Running K-Means with k =4  until misclassification
centroids, labels = kmeans(X = data, k = 4, centroids = 'kmeans++')

Ended at iteration 2

colors=np.array(['#2135CA','#A40227', '#598413', '#6C2DB3'])

fig, ax = plt.subplots(figsize=(8,5))  

ax.scatter(data[:,0],data[:,1], color = colors[labels])
ax.set_title('K-Means++', color = 'black', fontsize=16)

ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)

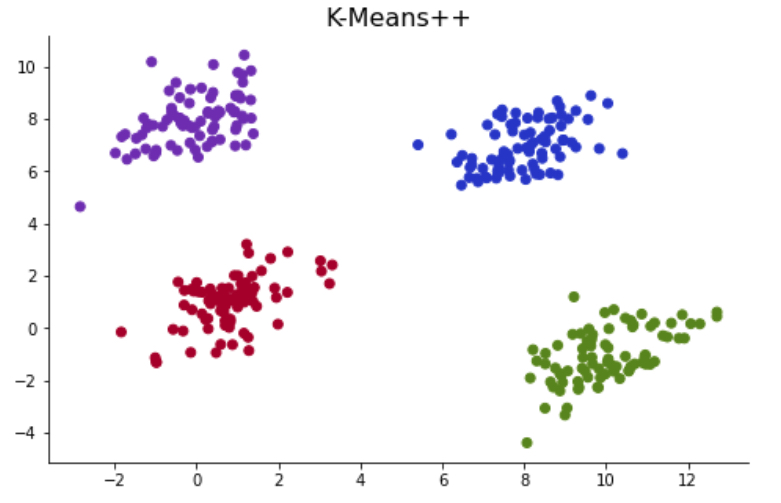
Notice that the clustering process ended at 1st iteration which is much shorter than that of basic K-Means. In addition, I was not able to reproduce the initiation problem with the K-Means++ method. You can also test it out!

Image Clustering

One of the interesting applications of the K Mean clustering is image compression into fewer colors. Since an image is an essential collection of numerical values indicating RGB colors, we can group similar colors using K-Means clustering. With this image compression process, the same image could be depicted with less data (k number of different colors) while the content of the image is mostly the same. This could be a useful pre-processing step for the image classification model.

Now, let’s import an image and color compress it.

from PIL import Image
import time

img = Image.open('./data/bar_medium.jpg') 
width = img.size[0]
height = img.size[1]
img

start_time = time.time()

X = np.array(img.getdata()) # Converting Image of Numpy Matrix

centroids, labels = kmeans(X, k=30, centroids='kmeans++', tolerance=.01) 

end_time = time.time()

print("--- %s seconds ---" % (time.time() - start_time))

Max Iteration Reached
--- 1559.3590371608734 seconds ---

centroids = centroids.astype(np.uint8)
X = centroids[labels] # reassign all points
img_ = Image.fromarray(X.reshape((height,width,3))) # Converting Numpy Matrix back to image type
img_

Choosing best k: Elbow Method

For the data like the Iris dataset, we already knew the number of clusters that we expected to observe. However, there are more cases where we do not have enough contextual knowledge regarding the data to pre-determine how many k clusters are optimal for the given data. The Elbow method is one of the most common approaches to determine the best number of clusters, k. It uses WCSS (Within-Cluster Sum of Squares) to find the k where an increase in k starts to minimally decrease the WCSS. Here are the steps of the elbow method:

1. Calculate WCSS (Within-Cluster Sum of Squares) for cluster k = 1.
2. Repeat for all reasonable range of k (typically 1 - 10)
3. Plot number of clusters vs. WCSS score
4. Find the elbow point where an increase in k does not reduce the WCSS score significantly

In the code below, I have demonstrated the elbow method using the Iris dataset:

from sklearn import datasets

# Loading Iris Data
Iris = datasets.load_iris()
X = Iris.data
y = Iris.target

def elbow_plot(X, max_k):
    
    WCSS_list = [] # bucket to collect WCSS

    for k in range(1, max_k+1):
        
        centroids, labels = kmeans(X = X, k = k, verbose = False)
        sum_of_squares = 0 
        
        for cid, c in enumerate(centroids): 
            X_class_c = X[labels == cid] # Selecting only rows corresponding to cluster with centroid c
            
            for row in X_class_c: # for every record in cluster c, calculate the distance and sum them together
                euc_dist = np.linalg.norm(row - c)
                sum_of_squares += euc_dist**2

        WCSS_list.append(sum_of_squares)
    
    fig, ax = plt.subplots(figsize=(13,7))  

    ax.plot(range(1, max_k+1), WCSS_list, color = '#476ba6', lw=1.5)
    ax.set_title('Elbow Plot', color = 'black', fontsize=16)
    ax.set_xlabel("Value of k", color = 'black', fontsize=14)
    ax.set_ylabel("WCSS Score", fontsize=14)
    
    ax.spines['top'].set_visible(False)
    ax.spines['right'].set_visible(False)

elbow_plot(X, 10)

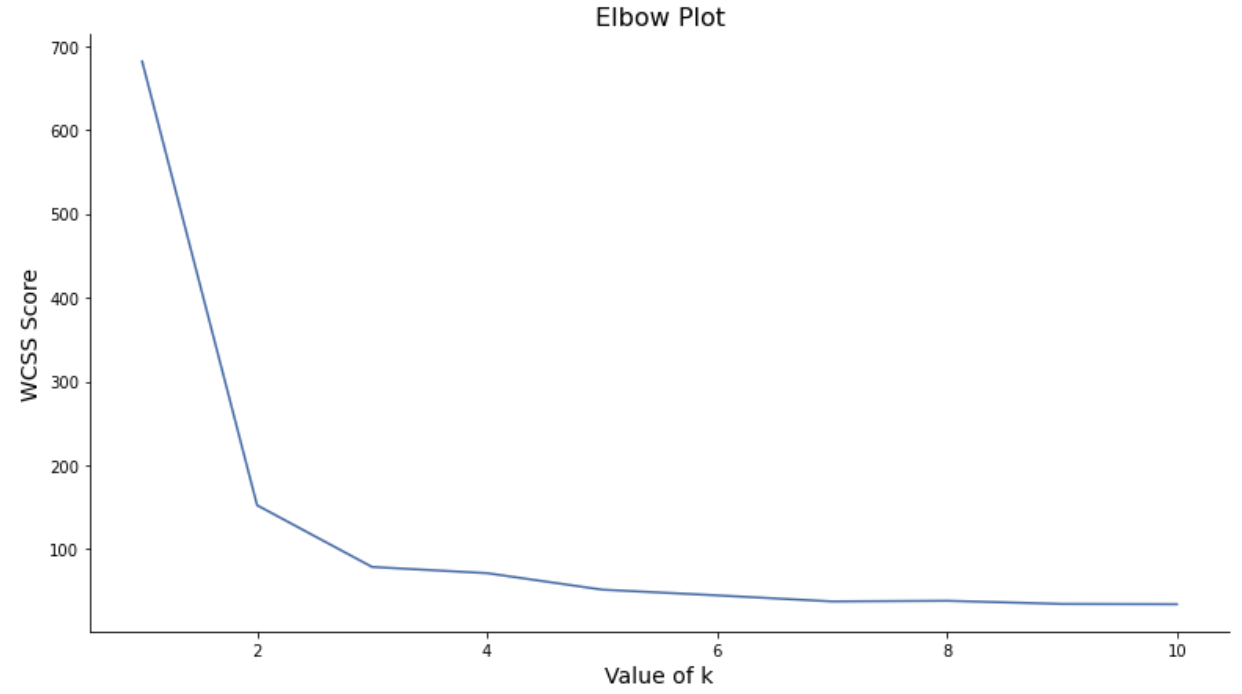
The elbow plot above depicts that after k=3, the calculated WCSS value converges and the plot is relatively flat. Therefore, we can conclude that the optimal numbrer of k is 3. We can verify the result with the number of labels in the dataset, which is 3.

Spectral Clustering

One of the drawbacks of K-Means clustering is that K-Means create circular boundaries by nature because it uses Euclidean distance to group data. To simplify, the K-Means effectively detects compact clusters and assumes that clusters are spherical. However, this assumption does not always hold to be true, and it fails to correctly cluster for the complex cluster that is shown below.

Another clustering technique called spectral clustering overcomes this problem by using connectivity between the nodes (data points). Instead of calculating the Euclidean distance between the chosen centroid and each data point, spectral clustering treats every data as a graph node, connecting each data point to the closest neighbors. And these nodes are converted into low-dimensional spectrums (eigenvalues).

from sklearn.datasets import make_circles

X, _ = make_circles(n_samples=500, noise=0.1, factor=.2)
centroids, labels = kmeans(X, 2, centroids='kmeans++', verbose=False)

colors=np.array(['#2135CA','#A40227'])

fig, ax = plt.subplots(figsize=(8,5))  

ax.scatter(X[:,0], X[:,1], color = colors[labels])
ax.set_title('Prediction Using K-Means', color = 'black', fontsize=16)

ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)

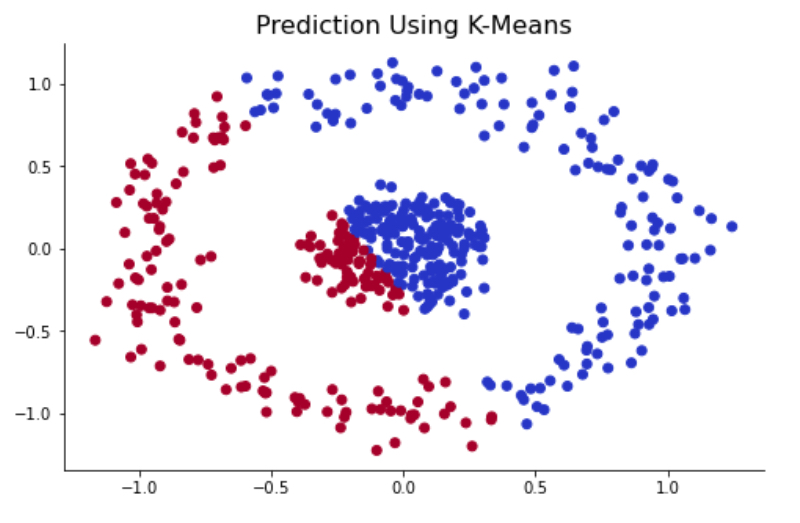
As you can see, the K-Means method was not able to capture two clusters correctly. This is due to the inherit nature of K-Means that uses Euclidean distance as its optimization process. Now let’s move on to the spectral clustering method and see its performance in this circle-in-circle dataset.

from sklearn.cluster import SpectralClustering


spec_clust = SpectralClustering(n_clusters=2,  affinity="nearest_neighbors").fit(X) #Spectral Clustering


colors=np.array(['#2135CA','#A40227'])

fig, ax = plt.subplots(figsize=(8,5))  

ax.scatter(X[:,0], X[:,1], color = colors[spec_clust.labels_])
ax.set_title('Prediction Using Spectral Clustering', color = 'black', fontsize=16)

ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)

/Users/kwonkh0424/opt/anaconda3/lib/python3.8/site-packages/sklearn/manifold/_spectral_embedding.py:245: UserWarning: Graph is not fully connected, spectral embedding may not work as expected.
  warnings.warn("Graph is not fully connected, spectral embedding"

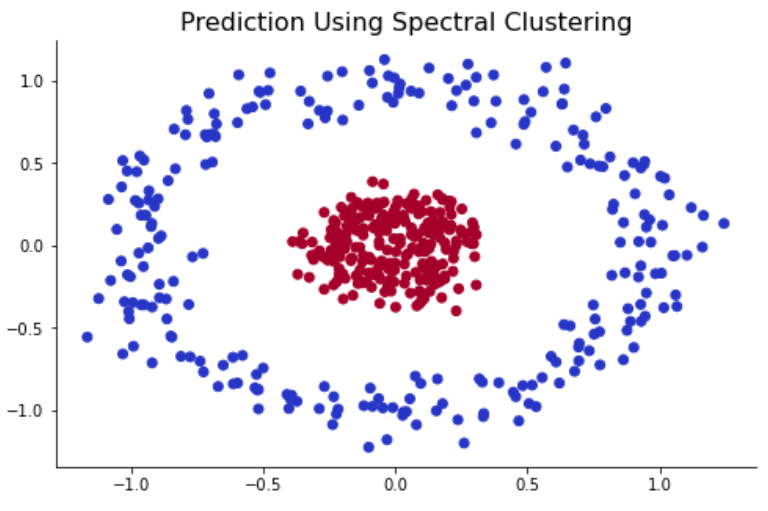
As shown above, spectral clustering was able to correclty identify two different clusters in the circle-in-circle dataset. Again, this is because the algorithm relies on graph node and edges to find the cluster and not minimal centroid and datapoint distance. </font>